跳转至

近似长方形的机器人碰撞检测优化

机器人是多边形，用12个圆形覆盖这个contour

优化问题

  • 优化变量：12个圆形的x, y, r
  • 目标函数：所有圆的并集（union_area）不属于 contour 部分的面积最小
  • 约束条件：
    • bound: -1 < x < 1, -1 < y < 0, r > 0.05
    • 所有圆的并集（union_area）和 contour的交集 (covered_area) 占 多边形的面积比大于98%

代码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
from scipy.optimize import minimize
from shapely.geometry import Point, Polygon
import matplotlib.pyplot as plt


# 定义多边形
polygon_coords = [
    (0.177, 0),
    (0.176, -0.0375),
    (0.175, -0.075),
    (0.165, -0.1125),
    (0.155, -0.15),
    (0.1335, -0.176),
    (0.112, -0.202),
    (0.06413, -0.202),
    (0.01626, -0.202),
    (-0.03161, -0.202),
    (-0.07948, -0.202),
    (-0.12735, -0.202),
    (-0.17522, -0.202),
    (-0.22309, -0.202),
    (-0.27096, -0.202),
    (-0.31883, -0.202),
    (-0.3667, -0.202),
    (-0.395, -0.1963),
    (-0.4115, -0.1739),
    (-0.428, -0.1515),
    (-0.432925, -0.113625),
    (-0.43785, -0.07575),
    (-0.442775, -0.037875),
    (-0.4477, 0),
    (-0.442775, 0.037875),
    (-0.43785, 0.07575),
    (-0.432925, 0.113625),
    (-0.428, 0.1515),
    (-0.4115, 0.1739),
    (-0.395, 0.1963),
    (-0.3667, 0.202),
    (-0.31883, 0.202),
    (-0.27096, 0.202),
    (-0.22309, 0.202),
    (-0.17522, 0.202),
    (-0.12735, 0.202),
    (-0.07948, 0.202),
    (-0.03161, 0.202),
    (0.01626, 0.202),
    (0.06413, 0.202),
    (0.112, 0.202),
    (0.1335, 0.176),
    (0.155, 0.15),
    (0.165, 0.1125),
    (0.175, 0.075),
    (0.176, 0.0375),
    (0.177, 0),
]
polygon = Polygon(polygon_coords)
polygon_area = polygon.area
print("多边形面积：", polygon_area)

# 圆的数量
num_circles = 12  # 可以根据需要调整这个值

# 初始化猜测
xs = [-0.13, -0.13, -0.03, -0.03, -0.23, -0.23, 0.07, 0.07, -0.33, -0.33, -0.34, 0.07]
ys = [0.1, -0.1, 0.1, -0.1, 0.1, -0.1, 0.1, -0.1, 0.1, -0.1, 0, 0]
rs = [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.11, 0.11]
initial_guess = xs + ys + rs

# 边界条件
x_bounds = [(-1, 1) for _ in range(num_circles)]
y_bounds = [(-1, 1) for _ in range(num_circles)]
r_bounds = [(0.05, None) for _ in range(num_circles)]
bounds = x_bounds + y_bounds + r_bounds


# 定义目标函数
def objective(vars):
    xs = vars[0:num_circles]
    ys = vars[num_circles : 2 * num_circles]
    rs = vars[2 * num_circles : 3 * num_circles]
    circles = [Point(xs[i], ys[i]).buffer(rs[i]) for i in range(num_circles)]
    union_area = circles[0]
    sum_area = circles[0].area
    for circle in circles[1:]:
        sum_area += circle.area
        union_area = union_area.union(circle)
    return union_area.area - union_area.intersection(polygon).area


def coverage_constraint(vars):
    xs = vars[0:num_circles]
    ys = vars[num_circles : 2 * num_circles]
    rs = vars[2 * num_circles : 3 * num_circles]
    circles = [Point(xs[i], ys[i]).buffer(rs[i]) for i in range(num_circles)]
    union_area = circles[0]
    for circle in circles[1:]:
        union_area = union_area.union(circle)
    covered_area = union_area.intersection(polygon).area
    return covered_area - 0.98 * polygon_area


# 约束条件
constraints = [
    {"type": "ineq", "fun": coverage_constraint},
]


# 执行优化
result = minimize(
    objective, initial_guess, method="SLSQP", bounds=bounds, constraints=constraints
)

# 解析结果
xs = result.x[0:num_circles]
ys = result.x[num_circles : 2 * num_circles]
rs = result.x[2 * num_circles : 3 * num_circles]

print("最优解：", result.fun)

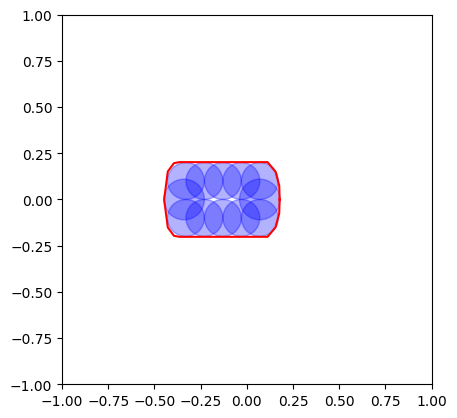
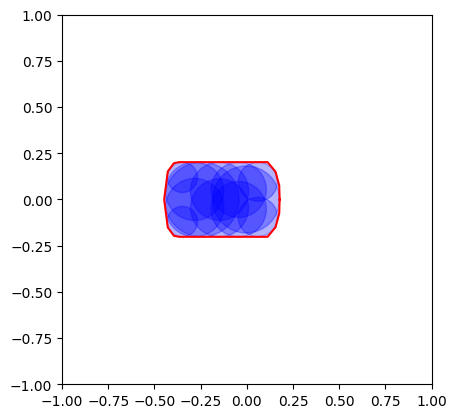
# 绘制结果
fig, ax = plt.subplots()
for x, y, r in zip(xs, ys, rs):
    print("x: ", x, "y: ", y, "r: ", r)
    circle = plt.Circle((x, y), r, color="blue", fill=True, alpha=0.3)
    ax.add_patch(circle)

x, y = polygon.exterior.xy
ax.plot(x, y, "r")
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_aspect("equal")
plt.show()

结果

  • 初始解 初始解
  • 最优解 最优解

初始解的选取很重要