基于搜索的路径规划
1. 图搜索基础
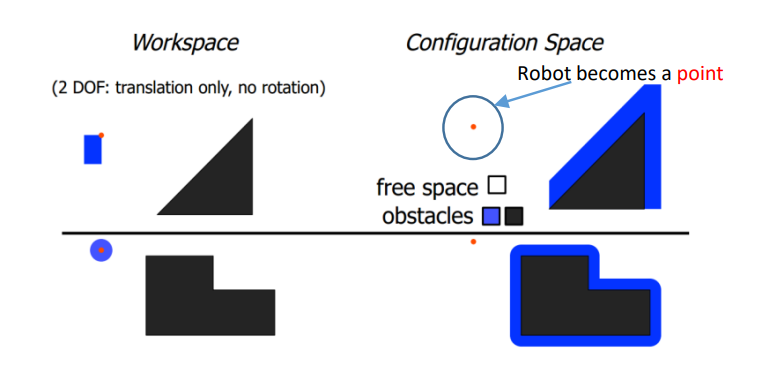
1.1 配置空间
一个n维空间，其中每一个点代表一个机器人的位姿
在配置空间中规划
1.2 图搜索
-
构建graph
- 栅格地图： 天然就是一个graph
- PRM: 随机采样点，然后连接成图
-
图搜索主循环
- 维护一个容器存储所有待访问的节点
- 容器初始节点为start
- 循环
- pop
- expansion
- push
- 结束循环
1.3 启发式搜索
存储节点，根据启发式函数排序
- 贪心搜索： \(f(n) = h(n)\)
- A*搜索： \(f(n) = g(n) + h(n)\)
- Dijkstra： \(f(n) = g(n)\)
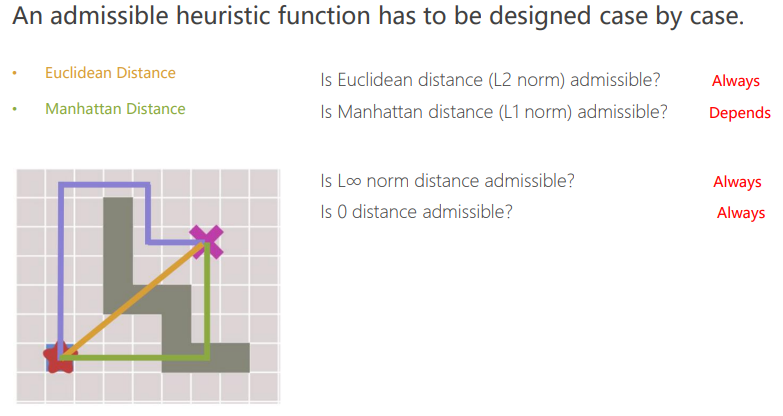
启发式函数：\(h(n)\) 估计从n到goal的代价
- 曼哈顿距离(L1 norm) \(dist = |x_1 - x_2| + |y_1 - y_2|\)
- 欧几里得距离(L2 norm) \(dist = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\)
- 切比雪夫距离(L∞ norm) \(dist = \max(|x_1 - x_2|, |y_1 - y_2|)\)
- 对角线距离 \(dist = |x_1 - x_2| + |y_1 - y_2| + (\sqrt{2} - 2) * \min(|x_1 - x_2|, |y_1 - y_2|)\)
Admissible启发式函数：\(h(n) \leq h^*(n)\)
1.4 Tie Breaker 技巧
搜索过程中，很多节点有相同的\(f(n)\)值，此时可以进行tie-breaker，打破路径中的对称性
-
稍微增大\(h(n)\)
\(h(n) = 1.0001 * h(n)\)
会影响 Admissible 性质吗？
不过由于环境中存在很多障碍物，\(h(n)\) 往往是小于实际代价的，因此几乎不会影响最优解
-
\(h(n) = h(n) + cross * 0.001\)
\[ dx1 = |node.x - end.x|, dy1 = |node.y - end.y| \\ dx2 = |start.x - end.x|, dy2 = |start.y - end.y| \\ cross = abs(dx1 * dy2 - dx2 * dy1) \] -
如果\(f(n)\)相同，对\(h(n)\)进行排序
2. Dijkstra和A*算法
2.1 Dijkstra算法
\(g(n)\): 从start到n的最少代价
2.2 A*算法
2.3 Weighted A*
\(f(n) = g(n) + \epsilon \cdot h(n), \epsilon > 1\)
- \(\epsilon = 1\) 时，等价于A*
- \(\epsilon > 1\) 时，更倾向于贪心搜索
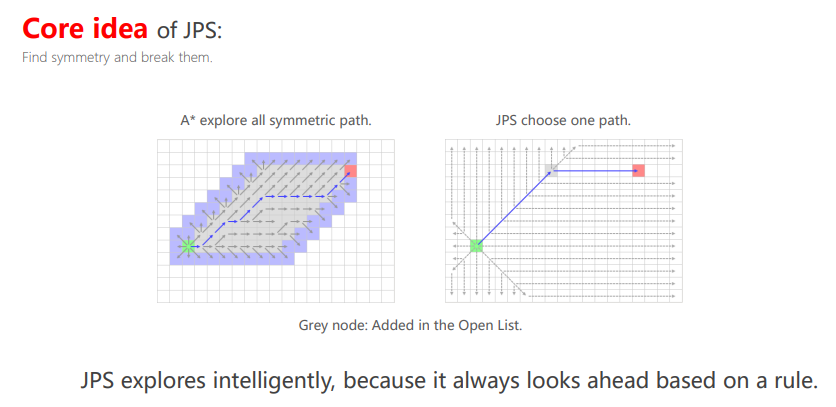
3. JPS算法（Jump Point Search）
JPS算法可以系统性地抵消图搜索中的对称性问题，和A*算法的区别是扩展邻居的方式不同
- A*算法： 当前节点附近4领域或8领域
- JPS算法： 通过jump点来扩展邻居
JPS一定比A*好吗？
- 当环境障碍物很复杂时，JPS可以很容易找到跳跃点，从而减少open list中节点数量
- 但是当环境障碍物稀疏时，JPS需要遍历很多节点才能找到跳跃点（灰色部分），对于每个遍历的点都需要进行碰撞检测，反而增加了计算量