动力学约束下的运动规划

1. Kinodynamic: Kinematic + Dynamics

• Kinematic: 运动学，考虑避障
• Dynamics: 动力学，考虑力、力矩等动力学量

为什么需要在路径规划的时候考虑动力学约束？

考虑动力学约束搜索出的路径（绿色实线）与不考虑动力学约束搜索出的路径（紫色实线）的拓扑结构不同，会影响后续轨迹优化的结果

2. 状态栅格搜索算法 (State Lattice Planning)

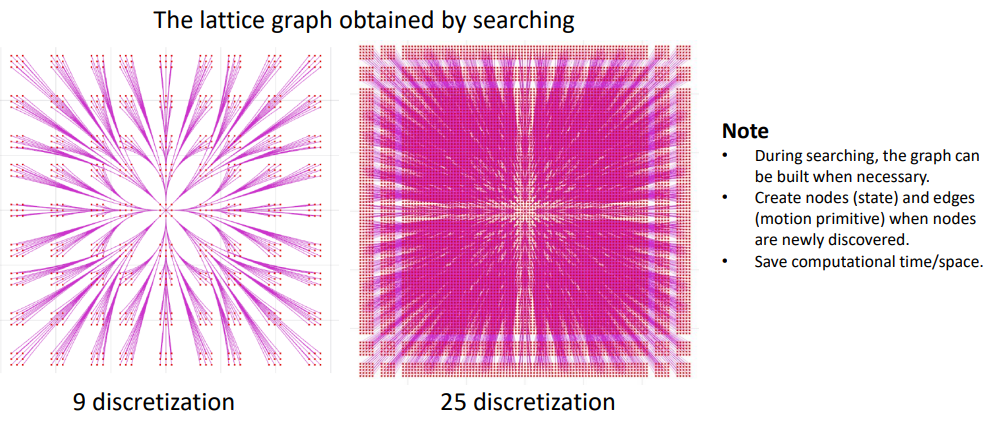
2.1 在控制空间采样

\(\dot{s} = f(s, u)\)，给定\(s_0\)，对输入\(u\)进行采样，得到\(s_1\)

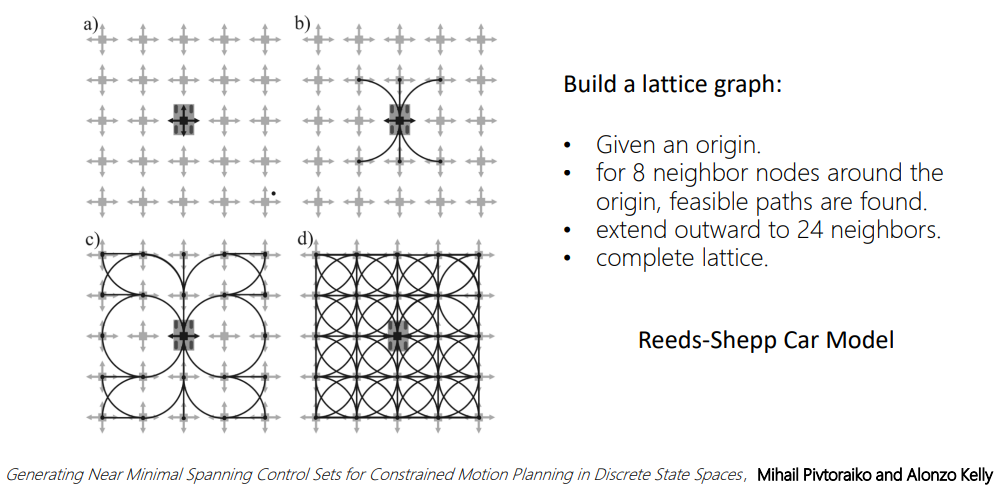
2.2 在状态空间采样

\(\dot{s} = f(s, u)\)，采样不同的\(s\)，计算\(u, T\)

3.两点边界值最优控制问题 (BVP & OBVP)

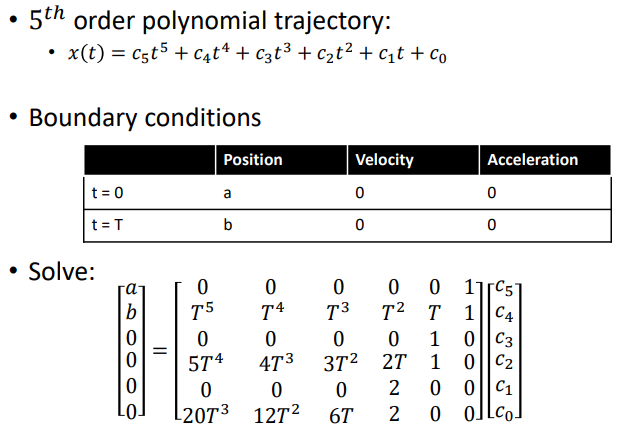
3.1 BVP (Boundary Value Problem)

3.2 OBVP (Optimal Boundary Value Problem)

3.2.1 建模

目标：\(\min J_{\sum} = \sum_{k=1}^{3} J_k, J_k = \frac{1}{T}\int_0^T j_k(t)^2dt\) 状态: \(s_k = (p_k, v_k, a_k)\) 输入: \(u_k = j_k(t)\) 系统模型: \(\dot{s}_k = f_s(s, u) = (v, a,j)\)