常微分方程简介
1. 常微分方程的定义
k阶常微分方程 (ODE of order k):
\[ F(t, x, \dot{x}, ..., x^{(k)}) = 0 \]
1.1 autonomous ODE
- autonomous ODE: \(\dot{x} = w(t, x)\)
- non-autonomous ODE: \(\dot{x} = v(x)\)
1.2 homogeneous ODE
- homogeneous ODE: \(\dot{x} = A(t)v(x)\)
- non-homogeneous ODE: \(\dot{x} = A(t)v(x) + B(t)\)
1.3 linear ODE
- linear ODE: \(\dot{x} = A(t)x + B(t)\)
2. 高阶常微分方程到一阶常微分方程组
任意阶常微分方程都可以转换为一阶常微分方程组
- n 阶 autonomous ODE 可以转换为 n 个一阶 autonomous ODE
- n 阶 non-autonomous ODE 可以转换为 n+1 个一阶 autonomous ODE
假设有3阶 non-autonomous ODE 如下:
\[ \dddot{x} = cos(\ddot{x}) + \dot{x} ^ 2 + x - t ^ 4 \]
令
\[ \boldsymbol{y} = \begin{pmatrix} t \\ x \\ \dot{x} \\ \ddot{x} \end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \end{pmatrix} \]
则有:
\[
\begin{aligned}
\dot{y_0} &= 1 \\
\dot{y_1} &= y_2 \\
\dot{y_2} &= y_3 \\
\dot{y_3} &= cos(y_3) + y_2 ^ 2 + y_1 - y_0 ^ 4 \\
\end{aligned}
\]
由此,我们得到了一个一阶常微分方程组:
\[ \dot{\boldsymbol{y}} =\begin{pmatrix} \dot{y_0} \\ \dot{y_1} \\ \dot{y_2} \\ \dot{y_3} \end{pmatrix} = \begin{pmatrix} 1 \\ y_2 \\ y_3 \\ cos(y_3) + y_2 ^ 2 + y_1 - y_0 ^ 4 \end{pmatrix} \]
3. 常见常微分方程求解
Initial Value Problem
\[
\begin{aligned}
&\text{Given:} \\
&\quad \dot{x} = w(t, x) \quad w: \mathbb{R} \times \mathbb{R^n} \to \mathbb{R^n} \\
&\quad x(0) = x_0 \\
&\text{Find all} \\
&\quad \alpha: (t_0, t_1) \to \mathbb{R} \quad s.t. \quad \alpha(t_0) = x_0 \quad and \quad \alpha'(t) = w(\alpha(t))
\end{aligned}
\]
3.1 autonomous ODE 求解
例1:
\[
\begin{aligned}
&\dot{x} = \lambda x \quad x(0) = x_0 \neq 0 \\
&=> \frac{dx}{dt} = \lambda x \\
&=> \frac{dx}{x} = \lambda dt \\
&=> \int \frac{dx}{x} = \int \lambda dt \\
&=> ln|x| = \lambda t + C \\
&=> |\alpha(t)| = e^{\lambda t + C} = e^C e^{\lambda t} \\
&=> \fbox{ $\alpha(t) = x_0 e^{\lambda t} $ }
\end{aligned}
\]
例2:
\[
\begin{aligned}
&\quad \dot{x} = x^2 \quad x(0) = x_0 \neq 0 \\
&=> \frac{dx}{dt} = x^2 \\
&=> \frac{dx}{x^2} = dt \\
&=> \int \frac{dx}{x^2} = \int dt \\
&=> -\frac{1}{x} = t + C \\
&=> -\frac{1}{\alpha(t)} = t + C \\
&=> \fbox{ $\alpha(t) = -\frac{1}{t + C} $ }
\end{aligned}
\]
3.2 可分离变量 ODE 求解
\[ \dot{x} = g(t)h(x) \quad h(x_0) \neq 0 \]
例1:
\[
\begin{aligned}
&\quad \dot{x} = sin(t)e^x \quad x(0) = x_0 \\
&=> \frac{dx}{e^x} = sin(t)dt \\
&=> \int \frac{dx}{e^x} = \int sin(t)dt \\
&=> -e^{-x} = -cos(t) + C \\
&=> e^{-x} = cos(t) - C \\
&=> \fbox{ $\alpha(t) = ln(cos(t) - C) $ }
\end{aligned}
\]
3.3 线性 ODE 求解
\[
\begin{aligned}
&\quad \dot{x} + A(t)x = B(t) \\
&=> \dot{x}e^{A(t)} + A(t)e^{A(t)}x = B(t)e^{A(t)} \\
&=> \frac{d}{dt}(e^{A(t)}x) = B(t)e^{A(t)} \\
&=> \int \frac{d}{dt}(e^{A(t)}x) dt = \int B(t)e^{A(t)} dt \\
&=> e^{A(t)}x = \int B(t)e^{A(t)} dt + C \\
&=> \fbox{ $\alpha(t) = e^{-A(t)}(\int B(t)e^{A(t)} dt + C) $ }
\end{aligned}
\]
4. 常微分方程解的性质
4.1 Lipschitz Continuity
Lipschitz Continuity
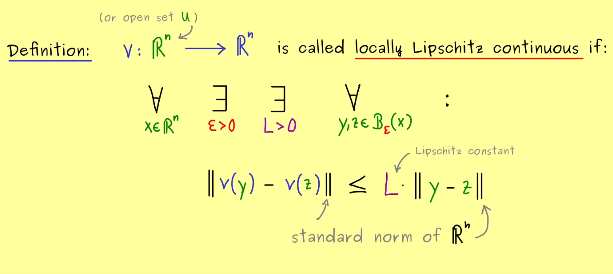
4.2 Banach Fixed Point Theorem
Banach Fixed Point Theorem

4.3 Picard-Lindelöf Theorem(for autonomous ODE)
Picard-Lindelöf Theorem for autonomous ODE

证明方式:
利用Lipschitz连续性,构造压缩映射(Contraction),利用Banach Fixed Point Theorem证明解的存在性和唯一性
Picard Iteration

使用Picard迭代法求解常微分方程
例1:
\[
\begin{aligned}
&\dot{x} = x \quad x(0) = 1 \\
&\text{start with: } \alpha: (-\epsilon, \epsilon) \to \mathbb{R} \quad \alpha(t) = 1 \\
&\text{first step: } \Phi(\alpha)(t) = 1 + \int_0^t \alpha(s) ds = 1 + t\\
&\text{second step: } \Phi^2(\alpha)(t) = 1 + \int_0^t (1 + s) ds = 1 + t + \frac{t^2}{2} \\
&\text{n-th step: } \Phi^n(\alpha)(t) = 1 + t + \frac{t^2}{2} + ... + \frac{t^n}{n!} = \sum_{k=0}^{n} \frac{t^k}{k!} \ = e^t \\
\end{aligned}
\]
4.4 Picard-Lindelöf Theorem(for non-autonomous ODE)
Picard-Lindelöf Theorem for non-autonomous ODE

Picard Iteration for non-autonomous ODE (special version)
特别的,当\(w: \mathbb{R} \times \mathbb{R^n} \to \mathbb{R^n}\) 是 Lipschitz continuous 时,Initial Value Problem 存在唯一的全局解

4.5 解的拓展、最大解、全局解(Extension of Solution, Maximal Solution, Global Solution)
-
解的拓展(Extension of Solution)
如果存在 $ I \supsetneq (t_0 - \epsilon, t_0 + \epsilon) $ 使得 $ \tilde{\alpha} |_{(t_0 - \epsilon, t_0 + \epsilon)} = \alpha $,则称 $ \tilde{\alpha} $ 是 $ \alpha $ 的拓展
-
最大解(Maximal Solution)
如果一个解 $ \alpha $ 不能被其他解拓展,则称 $ \alpha $ 是最大解
Note
对于4.3中的Initial Value Problem,存在唯一的最大解
证明方式:
利用Picard-Lindelöf Theorem证明
-
全局解(Global Solution)
如果最大解定义域 \(I = \mathbb{R}\),则称该解为全局解
4.6 IVP解的类型
对于4.3中的IVP,其最大解只有以下三种形式:
- 单射(Injective)
- 定点(Fixed Point)
- 周期(Periodic)
Quote


5. 线性微分方程组
\[ \boldsymbol{\dot{x}} = \boldsymbol{A}(t)\boldsymbol{x} + \boldsymbol{B}(t) \]
5.1 齐次线性微分方程组解空间
\[
\fbox
{
$
\begin{aligned}
&\text{对应齐次系统的解集:} \\
&S_0 = \{ \alpha: I \to \mathbb{R^n} \quad | \quad \alpha(t) = \boldsymbol{\dot{x}} = \boldsymbol{A}(t)\boldsymbol{x} \quad\text{for all} \quad t \in I \} \\
&\text {构成一个 n 维的 $\mathbb{R}$-向量空间}
\end{aligned}
$
}
\]
5.2 线性微分方程组的解
\[
\fbox{
$
\begin{aligned}
&\boldsymbol{\dot{x}} = \boldsymbol{A}(t)\boldsymbol{x} + \boldsymbol{B}(t) \text{ 的解集为: } \\
&\quad \quad S = S_0 + \gamma \\
&\text{其中: } \space S_0 \text{ 为齐次线性微分方程组的解集} \\
&\quad \quad \quad \gamma \text{ 为非齐次线性微分方程组的一个特解}
\end{aligned}
$
}
\]
6. 数值解法
6.1 Euler Method
\[
\begin{aligned}
&\dot{x}(t) \approx \frac{x(t + h) - x(t)}{h} \\
&=> \quad x(t + h) \approx x(t) + h \dot{x}(t) \\
&=> \quad x(t + h) \approx x(t) + h w(t, x(t))
\end{aligned}
\]
6.2 Backward Euler Method
\[
\begin{aligned}
&\dot{x}(t) \approx \frac{x(t) - x(t - h)}{h} \\
&=> \quad x(t) \approx x(t - h) + h \dot{x}(t) \\
&=> \quad x(t) \approx x(t - h) + h w(t, x(t))
\end{aligned}
\]
反向欧拉法是隐式方法,这是说需要求解一个方程才能得到新值 $ x_{n+1} $。通常用定点迭代或牛顿-拉弗森法(的某种修改版)实现之
6.3 显式 Runge-Kutta Method
\[
x_{n+1} = x_n + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4)
\]
其中:
\[
\begin{aligned}
k_1 &= w(t_n, x_n) \\
k_2 &= w(t_n + \frac{h}{2}, x_n + \frac{h}{2}k_1) \\
k_3 &= w(t_n + \frac{h}{2}, x_n + \frac{h}{2}k_2) \\
k_4 &= w(t_n + h, x_n + hk_3) \\
\end{aligned}
\]