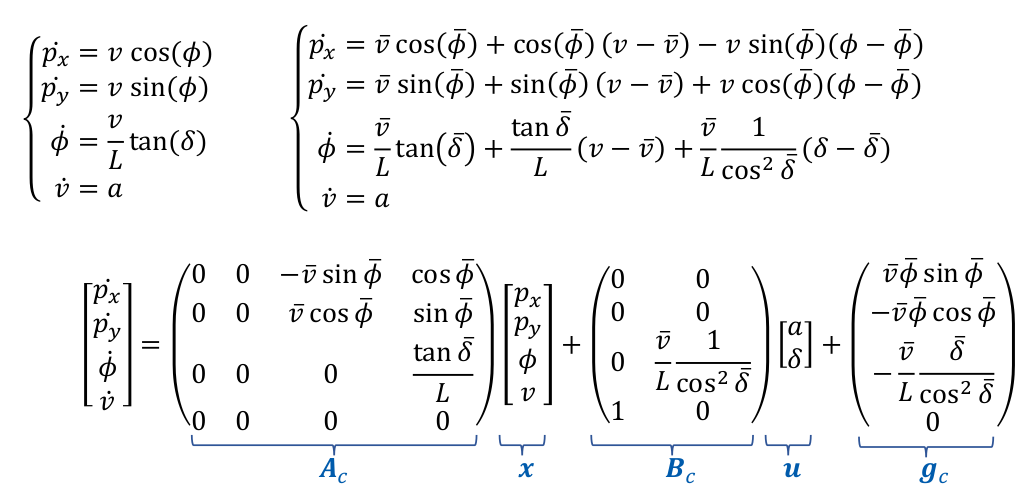MPC控制自行车模型沿轨迹运动
1. 运动学自行车模型(Kinematic Bicycle Model)
\[
\boldsymbol{\dot{x}} = \begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\phi} \\ \dot{v} \end{bmatrix} = \begin{bmatrix} v \cos(\phi) \\ v \sin(\phi) \\ \frac{v}{L} \tan(\delta) \\ a \end{bmatrix} = f(\boldsymbol{x}, \boldsymbol{u}), \quad \boldsymbol{x} = \begin{bmatrix} x \\ y \\ \phi \\ v \end{bmatrix}, \quad \boldsymbol{u} = \begin{bmatrix} a \\ \delta \end{bmatrix}
\]
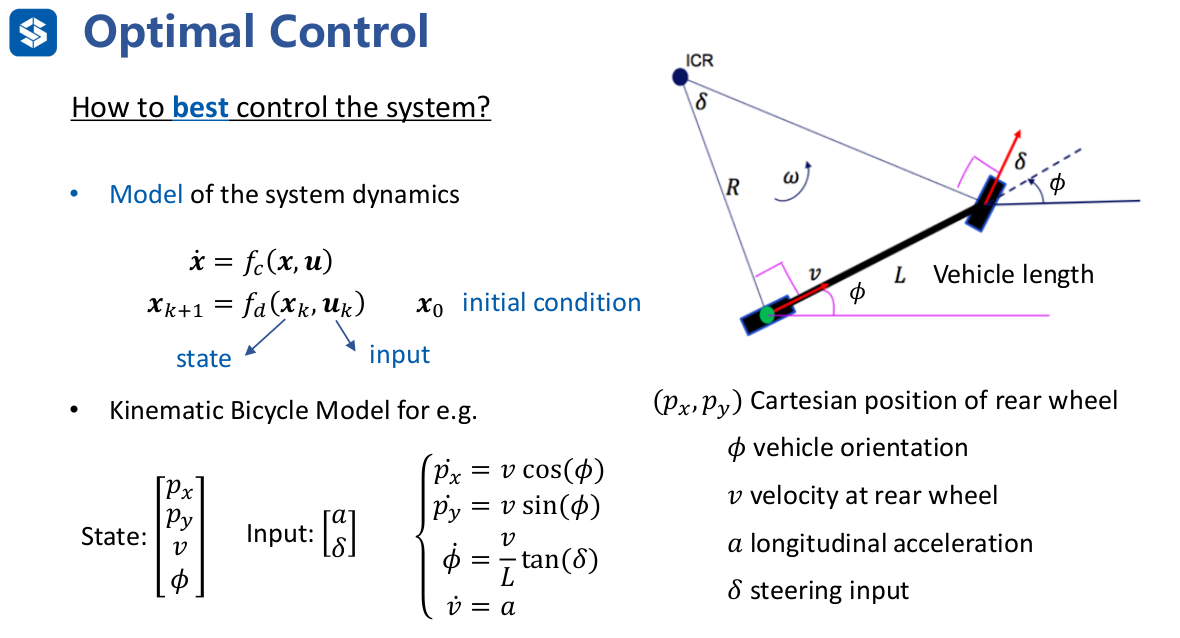
2. 非线性时变模型线性化
如1所示,自行车模型是一个非线性时变模型,我们希望将其线性化,当系统的状态\(x=\overline{\boldsymbol{x}}\),输入\(u=\overline{\boldsymbol{u}}\)时,有:
\[
\boldsymbol{\dot{x}} = f(\overline{\boldsymbol{x}}, \overline{\boldsymbol{u}}) + \frac{\partial f}{\partial \boldsymbol{x}} (\boldsymbol{x} - \overline{\boldsymbol{x}}) + \frac{\partial f}{\partial \boldsymbol{u}} (\boldsymbol{u} - \overline{\boldsymbol{u}}) = A_c \boldsymbol{x} + B_c \boldsymbol{u} + g_c
\]
根据线性化公式,我们可以得到线性化以后的自行车模型:
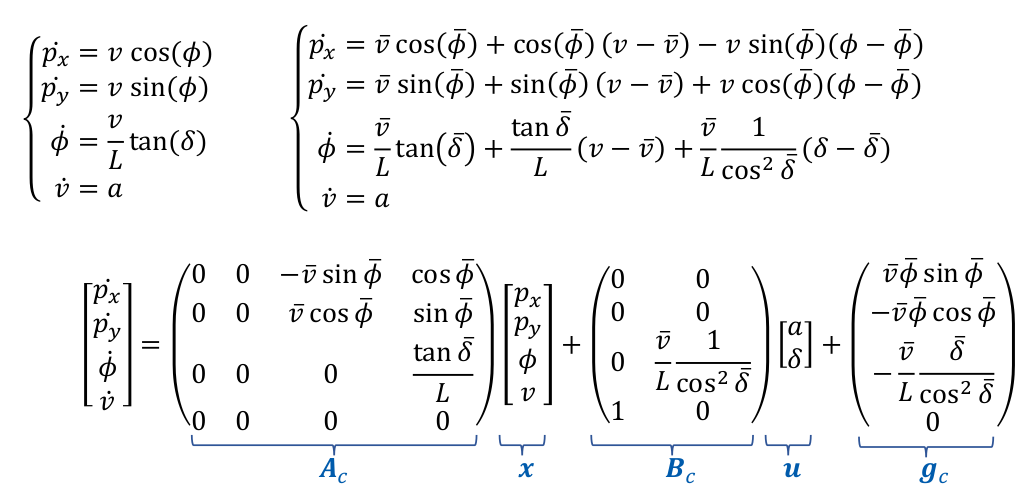
3. 线性时变模型离散化
\[
\begin{aligned}
\boldsymbol{\dot{x}} &= A_c \boldsymbol{x} + B_c \boldsymbol{u} + g_c \\
\frac{\boldsymbol{x}_{k+1} - \boldsymbol{x}_k}{T_s} &= A_c \boldsymbol{x}_k + B_c \boldsymbol{u}_k + g_c \\
\boldsymbol{x}_{k+1} &= (\boldsymbol{I} + T_s A_c) \boldsymbol{x}_k + T_s B_c \boldsymbol{u}_k + T_s g_c \\
\boldsymbol{x}_{k+1} &= A_d \boldsymbol{x}_k + B_d \boldsymbol{u}_k + g_d
\end{aligned}
\]
\[
\boldsymbol{x}_{k+1} = A_d \boldsymbol{x}_k + B_d \boldsymbol{u}_k + g_d \\
其中:A_d = \boldsymbol{I} + T_s A_c, \quad B_d = T_s B_c, \quad g_d = T_s g_c
\]
4. 成本函数(Cost Function)
成本函数一般由状态转移成本和终端状态成本组成:
\[
J = \sum_{k=0}^{N-1} q(\boldsymbol{x}_k, \boldsymbol{u}_k) + p(\boldsymbol{x}_N)
\]
在本次任务中,我们希望自行车模型沿着轨迹运动,因此我们希望小车当前位置误差和朝向误差最小,即:
\[
q(\boldsymbol{x}_k, \boldsymbol{u}_k) = (x_{k+1} - x_{k+1}^{ref})^2 + (y_{k+1} - y_{k+1}^{ref})^2 + \rho(\phi_{k+1} - \phi_{k+1}^{ref})^2
\]
同时,为了保持系统的稳定性,加上终端状态成本(TODO:MPC stability and feasibility):
\[
p(\boldsymbol{x}_N) = \rho_N (x_N - x_N^{ref})^2 + \rho_N (y_N - y_N^{ref})^2 + (v_N - v_N^{ref})^2 + \rho*\rho_N (\phi_N - \phi_N^{ref})^2
\]
因此我们定义:
\[
X = \begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_{N-1} \end{bmatrix},
X_{ref} = \begin{bmatrix} x_1^{ref} \\ x_2^{ref} \\ \cdots \\ x_{N-1}^{ref} \end{bmatrix},
U = \begin{bmatrix} u_0 \\ u_1 \\ \cdots \\ u_{N} \end{bmatrix}
\]
\[
\boldsymbol{Q}=\quad
\begin{pmatrix}
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & \rho & 0 \\
0 & 0 & 0 & 0 \\
\end{bmatrix} \\
&
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & \rho & 0 \\
0 & 0 & 0 & 0
\end{bmatrix} \\
& & \ddots \\
& & &
\begin{bmatrix}
\rho_N & 0 & 0 & 0 \\
0 & \rho_N & 0 & 0 \\
0 & 0 & \rho*\rho_N & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\end{pmatrix}
\]
则有:
\[
J = \frac{1}{2}(X - X_{ref})^T \boldsymbol{Q} (X - X_{ref})
\]
5. 约束条件(Constraints)
\[
\begin{aligned}
-v_{max} \leq &v_k \leq v_{max} \\
-a_{max} \leq &a_k \leq a_{max} \\
-\delta_{max} \leq &\delta_k \leq \delta_{max} \\
-\dot{\delta}_{max} \leq &\dot{\delta}_k \leq \dot{\delta}_{max}
\end{aligned}
\]
上述约束条件中\(v_k\)是状态变量,\(a_k\)、\(\delta_k\)是控制变量,而\(\dot{\delta}_k\)既不是状态变量也不是控制变量,因此需要进行转换
\[
\begin{aligned}
&\dot{\delta}_k = \frac{\delta_{k} - \delta_{k-1}}{T_s} \\
=> - &\delta_{max}*T_s \leq \delta_{k} - \delta_{k-1} \leq \delta_{max}*T_s
\end{aligned}
\]
5.1 状态变量的线性约束
\[
\boldsymbol{l}_x \leq \boldsymbol{C}_x X \leq \boldsymbol{u}_x
\]
其中
\[
\boldsymbol{l}_x =
\begin{pmatrix}
-v_{max} \\
-v_{max} \\
\vdots \\
-v_{max}
\end{pmatrix}
\boldsymbol{u}_x =
\begin{pmatrix}
v_{max} \\
v_{max} \\
\vdots \\
v_{max}
\end{pmatrix}
\boldsymbol{C}_x =
\begin{pmatrix}
\begin{bmatrix}
0 & 0 & 0 & 1
\end{bmatrix} \\
& \ddots \\
& & \begin{bmatrix}
0 & 0 & 0 & 1
\end{bmatrix}
\end{pmatrix}
\]
5.2 控制变量的线性约束
\[
\boldsymbol{l}_u \leq \boldsymbol{C}_u U \leq \boldsymbol{u}_u
\]
其中
\[
\scriptsize
\boldsymbol{l}_u =
\begin{pmatrix}
\begin{bmatrix}
-a_{max} \\ -\delta_{max} \\ -\delta_{max}*T_s
\end{bmatrix} \\
\begin{bmatrix}
-a_{max} \\ -\delta_{max} \\ -\delta_{max}*T_s
\end{bmatrix} \\
\vdots \\
\begin{bmatrix}
-a_{max} \\ -\delta_{max} \\ -\delta_{max}*T_s
\end{bmatrix}
\end{pmatrix}
\boldsymbol{u}_u =
\begin{pmatrix}
\begin{bmatrix}
a_{max} \\ \delta_{max} \\ \delta_{max}*T_s
\end{bmatrix} \\
\begin{bmatrix}
a_{max} \\ \delta_{max} \\ \delta_{max}*T_s
\end{bmatrix} \\
\vdots \\
\begin{bmatrix}
a_{max} \\ \delta_{max} \\ \delta_{max}*T_s
\end{bmatrix}
\end{pmatrix}
\boldsymbol{C}_u =
\begin{pmatrix}
\begin{bmatrix}
1 & 0 \\
0 & 1 \\
0 & 1
\end{bmatrix}
& & \\
\begin{bmatrix}
0 & 0 \\
0 & 0 \\
0 & -1
\end{bmatrix} &
\begin{bmatrix}
1 & 0 \\
0 & 1 \\
0 & 1
\end{bmatrix} \\
& & \ddots \\
& &
\begin{bmatrix}
0 & 0 \\
0 & 0 \\
0 & -1
\end{bmatrix} &
\begin{bmatrix}
1 & 0 \\
0 & 1 \\
0 & 1
\end{bmatrix}
\end{pmatrix}
\]
6. 使用OSQP求解二次规划问题
由于我们需要求解的变量是\(U\), 因此需要使用系统状态方程将\(X\)表示为\(U\)的函数:
由3中的线性时变模型离散化公式,需要注意,将系统线性化的过程是基于当前状态的,即每个\(x_{k+1}\)对应的\(A_d、B_d、g_d\)都是不同的,以下分别记为\(A_k、B_k、g_k\),则有:
\[
\begin{aligned}
\boldsymbol{x}_1 &= A_0 \boldsymbol{x}_0 + B_0 \boldsymbol{u}_0 + g_0 \\
\boldsymbol{x}_2 &= A_1 \boldsymbol{x}_1 + B_1 \boldsymbol{u}_1 + g_1 = A_1 A_0 \boldsymbol{x}_0 + A_1 B_0 \boldsymbol{u}_0 + A_1 g_0 + B_1 \boldsymbol{u}_1 + g_1 \\
\vdots \\
\boldsymbol{x}_N &= A_{N-1} \boldsymbol{x}_{N-1} + B_{N-1} \boldsymbol{u}_{N-1} + g_{N-1}
\end{aligned}
\]
由此可得
\[
X = A \boldsymbol{x}_0 + B U + G \\
\]
其中:
\[
\small
A = \begin{bmatrix}
A_0 \\
A_1 A_0 \\
\vdots \\
\prod_{k=0}^{N-1} A_k
\end{bmatrix}
B = \begin{bmatrix}
B_0 & 0 & \cdots & 0 & 0 \\
A_1 B_0 & B_1 & 0 & \cdots & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
\prod_{k=1}^{N-1} A_k B_0 & \prod_{k=2}^{N-1} A_k B_1 & \cdots & A_{N-1} B_{N-2} & B_{N-1}
\end{bmatrix}
G = \begin{bmatrix}
g_0 \\
A_1 g_0 + g_1 \\
\vdots \\
\sum_{k=0}^{N-2} (\prod_{i=k+1}^{N-1} A_i) g_k + g_{N-1}
\end{bmatrix}
\]
6.1 成本函数
由4中的成本函数,将上式带入,消去\(X\),得到:
\[
\begin{aligned}
J &= \frac {1}{2} (A \boldsymbol{x}_0 + B U + G - X_{ref})^T \boldsymbol{Q} (A \boldsymbol{x}_0 + B U + G - X_{ref}) \\
&= \frac {1}{2} (B U + (A \boldsymbol{x}_0 + G - X_{ref}))^T \boldsymbol{Q} (B U + (A \boldsymbol{x}_0 + G - X_{ref})) \\
&= \frac {1}{2} U^T B^T \boldsymbol{Q} B U + (A \boldsymbol{x}_0 + G - X_{ref})^T \boldsymbol{Q} B U + \frac {1}{2} (A \boldsymbol{x}_0 + G - X_{ref})^T \boldsymbol{Q} (A \boldsymbol{x}_0 + G - X_{ref}).
\end{aligned}
\]
只保留和\(U\)相关的项,得到:
\[
J = \frac {1}{2} U^T (B^T \boldsymbol{Q} B) U + (A \boldsymbol{x}_0 + G - X_{ref})^T \boldsymbol{Q} B U
\]
6.2 约束条件
将系统状态方程带入5.1式,得到:
\[
\begin{aligned}
\boldsymbol{l}_x \leq &\boldsymbol{C}_x X \leq \boldsymbol{u}_x \\
\boldsymbol{l}_x \leq &\boldsymbol{C}_x (A \boldsymbol{x}_0 + B U + G) \leq \boldsymbol{u}_x \\
\boldsymbol{l}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G \leq &\boldsymbol{C}_x B U \leq \boldsymbol{u}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G
\end{aligned}
\]
由此可得:
\[
\begin{bmatrix}
\boldsymbol{l}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G \\
\boldsymbol{l}_u
\end{bmatrix}
\leq
\begin{bmatrix}
\boldsymbol{C}_x B \\
\boldsymbol{C}_u
\end{bmatrix}
U
\leq
\begin{bmatrix}
\boldsymbol{u}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G \\
\boldsymbol{u}_u
\end{bmatrix}
\]
7. 系统时延处理
假设系统时延为\(\tau\), 则意味着当前时刻的控制量\(u(t)\)需要作用于\(t+\tau\)时刻的系统,如果我们把系统的初始状态\(\hat{x}_0\)定义成\(\tau\)时刻的状态,则同样可以利用之前所述内容进行求解。
对于一个系统\(\dot{x} = f(x, u), x(0) = x_0\), 求解其\(\tau\)时刻的状态\(x(\tau)\),可以使用Runge-Kutta方法进行数值求解,具体公式如下:
\[
x_{n+1} = x_n + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4)
\]
其中:
\[
\begin{aligned}
k_1 &= w(t_n, x_n) \\
k_2 &= w(t_n + \frac{h}{2}, x_n + \frac{h}{2}k_1) \\
k_3 &= w(t_n + \frac{h}{2}, x_n + \frac{h}{2}k_2) \\
k_4 &= w(t_n + h, x_n + hk_3) \\
\end{aligned}
\]